
技術コラム【吐出の羅針学】主な管路抵抗と計算式
塗布・充填装置は、一度に複数のワークや容器に対応できるよう、先端のノズルを分岐させることがよくあります。しかし、ノズルを分岐させ、それぞれの流量が等しくなるように設計するのは、簡単そうで結構難しいのです。今回は、分岐流量の求め方についてお話しする前に、まずは管路設計の基本である「主な管路抵抗と計算式」についてご説明します。以前のコラム「流路と圧力損失の関係」も参考にしながら、ご覧ください。
各種の管路抵抗
管路抵抗(損失)には主に、次のようなものがあります。
1.直管損失
管と流体の摩擦による損失で、最も基本的、かつ影響の大きい損失です。円管の場合、L を管長さ、d を管径、ρ を密度とし、流速を v とすると、
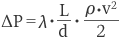
で表されます。
ここでλは管摩擦係数といい、層流の場合、Re をレイノルズ数として(詳しくは移送の学び舎「流体って何?(流体と配管抵抗))、
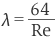
乱流の場合、
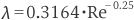
で表すことができます(※ブラジウスの式。乱流の場合、λは条件により諸式ありますので、また確認してみてください)。
2.入口損失
タンクなどの広い領域から管に流入する場合、損失が生じます。これを入口損失といい、
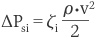
で表されます。
ζi は損失係数で、入口の形状により下図のような値となります。
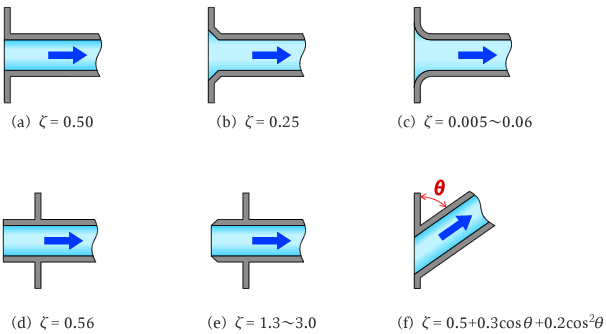
3.縮小損失
管断面が急に縮小するような管では、流れが収縮することによる縮流が生じ、損失が生じます。大径部および小径部の流速をそれぞれ v1、v2、断面積を A1、A2 とすると、
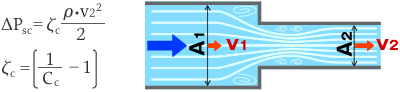
となります。CC は収縮係数と呼ばれ、CC とζC は次表で表されます。
| A2/A1 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 |
|---|---|---|---|---|---|---|---|---|---|---|
| CC | 0.61 | 0.62 | 0.63 | 0.65 | 0.67 | 0.70 | 0.73 | 0.77 | 0.84 | 1.00 |
| ζC | 0.41 | 0.38 | 0.34 | 0.29 | 0.24 | 0.18 | 0.14 | 0.089 | 0.036 | 0 |
上表においてA1 = ∞ としたとき、2.入口損失の(a)に相当することになる、即ち ζc = 0.5 になると考えることもできます。
4.拡大損失
管断面が急に拡大するような広がり管では、大きなはく離領域が起こり、はく離損失が生じます。小径部および大径部の流速をそれぞれ v1、v2、断面積を A1、A2 とすると、
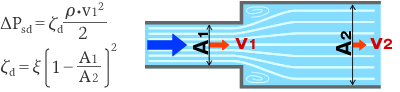
となります。
ξ は面積比 A1/A2 によって変化する係数ですが、ほぼ1となります。
5.出口損失
管からタンクなどの広い領域に流出する場合は、出口損失が生じます。管部の流速を v とすると、
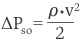
となります。
出口損失は4.拡大損失において、A2 = ∞ としたものに等しくなります。
6.曲がり損失(エルボ)
管が急に曲がる部分をエルボといい、はく離現象が起こり、損失が生じます。流速を v とすると、
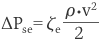
となります。
ζe は損失係数で、多数の実験結果から近似的に、θ をエルボ角度として、次式で与えられます。
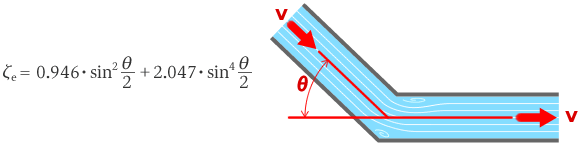
7.分岐管における損失
図のような分岐管の場合、本管1から支管2へ流れるときの損失 ΔPsb2 、本管1から支管3へ流れるときの損失 ΔPsb3 は、本管1の流速 v1 として、
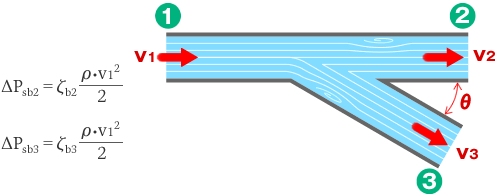
ただし、それぞれの損失係数 ζb2 、ζb3 は、分岐角度 θ 、分岐部の形状、流量比、直径比、Re数などに依存するため、実験的に求める必要があります。
